โอเปอเรชัน
1. คุณสมบัติปิด 
2. คุณสมบัติการเปลี่ยนกลุ่มได้ 
3. เอกลักษณ์มี  ซึ่งทำให้ ซึ่งทำให้ 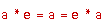 สำหรับ สำหรับ 
4. อินเวอร์ส สำหรับสมาชิก  แต่ละตัวจะมี แต่ละตัวจะมี
 ซึ่ง ซึ่ง 
|
การกระจายสัมพัทธ์
(relative variation) |
การวัดการกระจายของข้อมูลแต่ละชุด เพื่อนำไปใช้ในการเปรียบเทียบการกระจายกับข้อมูลชุดอื่น ๆ การกระจายสัมพัทธ์มี 4 ชนิดคือ
1. สัมประสิทธิ์ของพิสัย
2. สัมประสิทธิ์ของส่วนเบี่ยงเบนควอร์ไทล์
3. สัมประสิทธิ์ของส่วนเบี่ยงเบนเฉลี่ย
4. สัมประสิทธิ์ของการแปรผัน
|
การแจกแจงความถี่
(frequency distribution) |
รูปแบบการกระจายของความถี่ของค่าจากการสังเกตทั้งหมด
|
การแจงนับอย่างครบถ้วน
(complete enumeration) |
การเก็บรวบรวมข้อมูลของทุกหน่วยของประชากรที่สนใจศึกษา (ดู สำมะโน ประกอบ) |
การทดลองสุ่ม
(random experiment) |
การทดลองที่ทราบผลลัพธ์ว่าจะเป็นอะไรได้
บ้าง แต่ไม่สามารถจะพยากรณ์ผลที่จะเกิดขึ้นในแต่ละครั้งว่า จะเป็นอะไรในบรรดาผลลัพธ์ที่อาจเป็นได้เหล่านั้น
|
การแปรผกผัน
(inverse variation) |
เมื่อ x และ y แทนปริมาณใด ๆ y แปรผกผันกับ x เขียนแทนด้วยสัญลักษณ์ 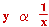 หมายถึง หมายถึง 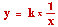 เมื่อ k เป็นค่าคงตัวและ k # 0 เมื่อ k เป็นค่าคงตัวและ k # 0
|
การแปรผันเกี่ยวเนื่อง
(joint variation) |
เมื่อ x, y และ z แทนปริมาณใด ๆ x แปรผันเกี่ยวเนื่องกับ y และ z แทนด้วยสัญลักษณ์  หมายถึง หมายถึง 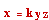 เมื่อ k เป็นค่าคงตัวและ k # 0 เมื่อ k เป็นค่าคงตัวและ k # 0
|
การแปรผันโดยตรง
(direct variation) |
เมื่อ x และ y แทนปริมาณใด ๆ y แปรผันโดยตรงเป็น x เขียนแทนด้วยสัญลักษณ์  หมายถึง หมายถึง 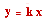 เมื่อ k เป็นค่าคงตัวและ k # 0 เมื่อ k เป็นค่าคงตัวและ k # 0
|
การสุ่มตัวอย่าง
(random sampling) |
การเลือกตัวอย่างสมาชิกของประชากรโดยที่ทุกสมาชิกในกลุ่มมีโอกาสได้รับเลือกเท่า ๆ กัน โดยไม่เจาะจง
|
กำลังสอง
(square) |
กำลังสองของจำนวนจริง x ใด ๆ หมายถึง  เขียนแทนด้วยสัญลักษณ์ เขียนแทนด้วยสัญลักษณ์ 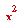 โดยมี 2 เป็นเลขชี้กำลัง โดยมี 2 เป็นเลขชี้กำลัง
|
กำลังสองสมบูรณ์
(perfect square) |
กำลังสองของจำนวนหรือของพหุนาม เช่น
4 เป็นกำลังสองสมบูรณ์ของ 2 และมีค่าเท่ากับ 22
a2 + 2ab + b2 เป็นกำลังสองสมบูรณ์ของ a + b และมีค่าเท่ากับ (a + b)2 |
กึ่งช่วงควอร์ไทล์
(semi - interquartile range) |
ดู ส่วนเบี่ยงเบนควอร์ไทล์ |
แกนจริง, แกนจำนวนจริง
(real axis ,real number axis) |
แกนนอนของระนาบเชิงซ้อน |
แกนจินตภาพ
(imaginary axis) |
แกนตั้งของระนาบเชิงซ้อน |
แกนวาย
(Y - axix) |
ดูในเรื่อง ระบบแกนมุมฉาก |
แกนสมมาตร
(axis of symmetry) |
เส้นตรง L จะเป็นแกนสมมาตรของจุด P และจุด Q เมื่อลากส่วนของเส้นตรง PQ แล้ว L จะแบ่งครึ่งและตั้งได้ฉากกับส่วนของเส้นตรง PQ และในกรณีนี้กล่าวได้ว่าจุด P สมมาตรกับจุด Q
L จะเป็นแกนสมมาตรของส้นโค้ง C หรือรูป A ใด ๆ เมื่อทุก ๆ จุดบนเส้นโค้งหรือบนรูปนั้นสมมาตรกันดูภาพประกอบ
รูปที่ 1. เส้นตรง L เป็นแกนสมมาตรของจุด P และ Q
รูปที่ 2. เส้นตรง L เป็นแกนสมมาตรของเส้นโค้ง C
รูปที่ 3. เส้นตรง L และ L' เป็นแกนสมมาตรของรูป A
|
แกนเอกซ์
(X - axis) |
ดูในเรื่อง ระบบแกนมุมฉาก |

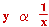 หมาย
หมาย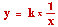 เมื่อ k เป็น
เมื่อ k เป็น หมาย
หมาย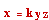 เมื่อ k เป็น
เมื่อ k เป็น หมาย
หมาย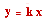 เมื่อ k เป็น
เมื่อ k เป็น เขียน
เขียน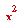 โดย
โดย