

 ความหมายของเซต ความหมายของเซต |  การเขียนเซต การเขียนเซต
 ลักษณะของเชต ลักษณะของเชต  ความสัมพันธ์ของเซต ความสัมพันธ์ของเซต
 สับเซต สับเซต  เพาเวอร์เซต เพาเวอร์เซต
 เอกภพสัมพัทธ์ เอกภพสัมพัทธ์  แผนภาพของเวนน์-ออยเลอร์ แผนภาพของเวนน์-ออยเลอร์
 ปฏิบัติการระหว่างเซต ปฏิบัติการระหว่างเซต  สัญลักษณ์ที่เกี่ยวข้องกับจำนวนต่าง ๆ ที่ควรทราบ สัญลักษณ์ที่เกี่ยวข้องกับจำนวนต่าง ๆ ที่ควรทราบ
|

| 1. | ยูเนียน (Union) | ยูเนียนของเซต A และ B คือเซตที่ประกอบด้วยสมาชิกของเซต A หรือ B เขียนแทนด้วย A  B B
2. | อินเตอร์เซคชัน (Intersection) | อินเตอร์เซคชันของเซต A และ B คือเซตที่ประกอบด้วยสมาชิกของเซต A และ B | เขียนแทนด้วย A  B B
3. | คอมพลีเมนต์ (Complement) | คอมพลีเมนต์ของเซต A คือเซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของเอกภพสัมพัทธ์ แต่ไม่เป็นสมาชิกของ A | เขียนแทนด้วย A' 4. | ผลต่างของเซต (Difference) | ผลต่างของเซต A และ B คือเซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A แต่ไม่เป็นสมาชิกของเซต B | เขียนแทนด้วย A - B |

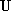 = {1, 2, 3, ..., 20},
A = {1, 2, 3, 4, 5, 6},
B = {2, 4, 6, 8, 10, 12} = {1, 2, 3, ..., 20},
A = {1, 2, 3, 4, 5, 6},
B = {2, 4, 6, 8, 10, 12} |
|||||||
|---|---|---|---|---|---|---|---|
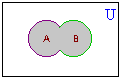 A  B = {1, 2, 3, 4, 5, 6, 8, 10, 12} B = {1, 2, 3, 4, 5, 6, 8, 10, 12}
| 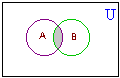 A  B = {2, 4, 6} B = {2, 4, 6}
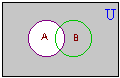 A' = {7, 8, 9, ..., 20} 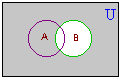 B' = {1, 3, 5, 7, 9, 11, ...,20} 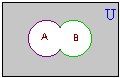 (A  B)' = {7, 9, 11, 13, ..., 20} B)' = {7, 9, 11, 13, ..., 20}
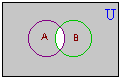 (A  B)' = {1, 3, 5, 7, ..., 20} B)' = {1, 3, 5, 7, ..., 20}
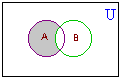 A - B = {1, 3, 5} 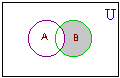 B - A = {8, 10, 12} | ||||||