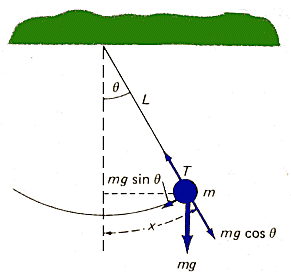
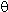 กับแนว
กับแนว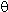 เป็น
เป็น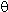 ดัง
ดัง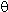 ก็
ก็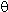 อยู่
อยู่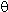 ซึ่ง
ซึ่ง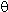 นี่
นี่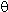
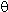 มี
มี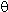 =
= 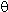
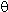
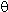 น้อย ๆ จึง
น้อย ๆ จึง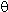
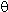 น้อย ๆ จะ
น้อย ๆ จะ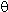 =
= 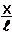
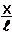
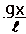
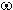 2x
2x
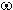 2x = g
2x = g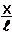
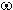 2 =
2 = 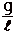
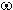 =
= 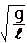
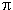 f
f
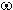 = 2
= 2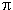 f =
f = 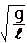
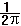
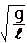 = ความถึ่ของการแกว่งของลูกตุ้ม
= ความถึ่ของการแกว่งของลูกตุ้ม
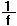 = 2
= 2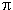
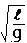 = คาบของการแกว่งของลูกตุ้ม
= คาบของการแกว่งของลูกตุ้ม
ที่มา : นายณสรรค์ ผลโภค, นิตยสารเรียนดี ปี 2 ฉบับที่ 3.
