แม่เหล็ก (magnet) เป็นสิ่งที่สามารถดูวัสดุบางชนิดได้ เช่น เหล็ก นิกเกิล โคบอลต์ เป็นต้น การที่แม่เหล็กดูดสารบางอย่างได้ เนื่องจากมีสนามแม่เหล็ก (magnetic field) ในบริเวณโดยรอบแม่เหล็ก เราสามารถตรวจสอบว่าบริเวณใดมีสนามแเม่เหล็กหรือไม่ โดยใช้เข็มทิศ แต่เราไม่สามารถทราบได้ว่ามีค่าเท่าใด นักวิทยาศาสตร์พยายามวัดสนามแม่เหล็กด้วยวิธีการต่าง ๆ แต่ในปัจจุบันเราสามารถวัดสนามแม่เหล็กได้สะดวกและรวดเร็วโดยใช้ตัวรับรู้ฮอลล์ (Linear Hall sensor) ซึ่งทำงานโดยอาศัยหลักการของปรากฏการณ์ฮอลล์ (Hall effect) ตัวรับรู้ฮอลล์เป็นวงจรรวมที่ทำให้เกิดความต่างศักย์ซึ่งเป็นสัดส่วนตรงกับความเข้มของสนามแม่เหล็กที่ผ่านในแนวดิ่ง เมื่อนำตัวรับรู้ฮอลล์ไปต่อกับโวลต์มิเตอร์ แล้วนำไปวางใกล้บริเวณที่มีสนามแม่เหล็กก็จะทำให้ทราบค่าความเข้มของสนามแม่เหล็กได้

ตัวรับรู้ฮอลล์ (Linear Hall sensor)


รูปที่ 1 ตัวรับรู้ฮอลล์

ตัวรับรู้ฮอลล์เป็นวงจรรวม มีขนาดและลักษณะดังรูปที่ 1 และมีสมบัติดังนี้

input voltage 4.5-6V offset voltage 2.5 V (ประมาณ) sensitivity 13 V/T

เมื่อต่อแหล่งจ่ายไฟกระแสตรงหรือเซลล์ไฟฟ้า 4.5-6 โวลต์ เข้ากับขา 1 และขา 2 และ ต่อโวลต์มิเตอร์เข้ากับขา 2 และขา 3 ดังรูปที่ 2 โวลต์มิเตอร์จะแสดงค่าประมาณ 2.5 โวลต์ ค่านี้เป็นความต่างศักย์ขณะที่ไม่มีสนามแม่เหล็ก เรียกว่า offset voltage ค่านี้อาจเปลี่ยนแปลงได้เล็กน้อยขึ้นอยู่กับโวลเตจของแหล่งจ่ายไฟกระแสตรงที่ต่อกับขา 1 และขา 2 แต่จะมีค่าประมาณครึ่งหนึ่งของโวลเตจของแหล่งจ่ายไฟกระแสตรง


รูปที่ 2 การต่อตัวรับรู้ฮอลล์กับแหล่งจ่ายไฟกระแสตรงและโวลต์มิเตอร์


รูปที่ 3 การวัดความเข้มของสนามแม่เหล็ก

เมื่อนำแม่เหล็กเข้าใกล้ active area ของตัวรับรู้ฮอลล์ ความต่างศักย์จะมีค่าเพิ่มขึ้นหรือลดลงขึ้นอยู่กับทิศของสนามแม่เหล็ก กล่าวคือถ้านำขั้วใต้เข้าใกล้ ความต่างศักย์จะมีค่าเพิ่มขึ้น แต่ถ้านำขั้วเหนือเข้าใกล้ ความต่างศักย์จะมีค่าลดลง ความต่างศักย์ที่เปลี่ยนไปมีความสัมพันธ์กับความเข้มของสนามแม่เหล็กหรือความหนาแน่นฟลักซ์แม่เหล็ก (magnetic flux density) ดังนี้

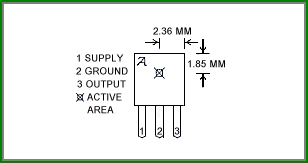
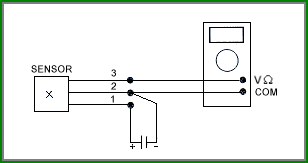
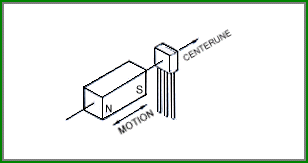
B = (Vout (B) - Vout (O) ) S-1 เมื่อ Vout (O) เป็นความต่างศักย์ขณะไม่มีสนามแม่เหล็ก Vout (B) เป็นความต่างศักย์ขณะมีสนามแม่เหล็ก S เป็นสัมประสิทธิ์ความไว มีหน่วยเป็นโวลต์ต่อเทสลา (V/T) สำหรับตัวรับรู้ฮอลล์ที่ใช้ในบทความนี้ S = 13 V/T B เป็นความเข้มของสนามแม่เหล็ก หรือความหนาแน่นฟลักซ์แม่เหล็ก มีหน่วยเป็นเทสลา (T)

ตัวรับรู้ฮอลล์สามารถวัดสนามแม่เหล็กในบริเวณใกล้แม่เหล็กถาวร สนามแม่เหล็กที่เกิดขึ้นบริเวณปลายโซเลนอยด์และสนามแม่เหล็กใกล้เส้นลวดตัวนำที่มีกระแสไฟฟ้าผ่านได้

ปรากฏการณ์ฮอลล์ (Hall Effect)

ใน ค.ศ. 1879 เอ็ดวิน ฮอลล์ (Edwin Hall) นักศึกษามหาวิทยาลัยจอห์น ฮอพคินส์ ซึ่งในขณะนั้นมีอายุ 24 ปี ได้พบว่า เมื่อนำแผ่นตัวนำบางที่มีกระแสไฟฟ้าผ่านไปวางไว้ในบริเวณที่มีสนามแม่เหล็ก พาหะประจุ (charge carriers) ในตัวนำสามารถเบนไปจากแนวทางเดิมได้ และการเบนนี้มีผลทำให้เกิดสนามไฟฟ้าในตัวนำบางในทิศตั้งฉากกับทั้งกระแสไฟฟ้าและสนามแม่เหล็ก การค้นพบนี้เรียกว่า ปรากฏการณ์ฮอลล์


รูป 1 ก-ค แสดงการเกิดปรากฏการณ์ฮอลล์

การเกิดปรากฏการณ์ฮอลล์อาจอธิบายได้โดยใช้รูป 1 ก-ค ดังนี้

รูป 1 ก แสดงแผ่นตัวนำบางที่มีความกว้าง d หนา t และมีกระแสไฟฟ้า (conventional current) I ผ่านในทิศจากด้านซ้ายไปด้านขวา พาหะประจุคืออิเล็กตรอนเคลื่อนที่ (ด้วยอัตราเร็วลอยเลื่อน V_d) ในทิศตรงข้ามกับกระแสไฟฟ้า I จากด้านขวาไปด้านซ้าย

รูป 1 ข เมื่อใส่สนามแม่เหล็ก B ในทิศพุ่งเข้าหาและตั้งฉากกับระนาบแผ่นตัวนำบางหรือกระดาษ จะเกิดแรงแม่เหล็ก F_B กระทำกับอิเล็กตรอน ทำให้อิเล็กตรอนเบนไปทางขอบด้านบนของแผ่นตัวนำบาง

รูป 1 ค เมื่อเวลาผ่านไปจะมีอิเล็กตรอนถูกผลักไปที่ขอบด้านบนจำนวนมาก ส่วนขอบด้านล่างจะเกิดประจุไฟฟ้าบวกจำนวนมากเช่นกัน การที่มีประจุไฟฟ้าต่างชนิดกันที่ขอบทั้งสอง ทำให้เกิดสนามไฟฟ้า เรียกว่า สนามไฟฟ้าฮอลล์ (hall field) E_H ในแผ่นตัวนำบางมีทิศจากขอบด้านล่างไปขอบด้านบน สนามไฟฟ้าจะทำให้เกิดแรงไฟฟ้า F_E กระทำกับอิเล็กตรอน ซึ่งจะทำให้อิเล็กตรอนถูกผลักไปทางขอบด้านล่าง เมื่อแรงไฟฟ้าและแรงแม่เหล็กมีขนาดเท่ากัน อิเล็กตรอนจะเคลื่อนที่ในทิศไปทางซ้ายโดยไม่เบน

สนามไฟฟ้าที่เกิดในแผ่นตัวนำบางมีความสัมพันธ์กับความต่างศักย์หรือโวลเตจ V ดังนี้

ความต่างศักย์หรือโวลเตจที่เกิดขึ้นนี้เรียกว่า ความต่างศักย์ฮอลล์ (hall potential difference หรือ hall voltage) V_H พบว่า ความต่างศักย์ฮอลล์มีค่ามากที่สุด เมื่อแผ่นตัวนำบางทำจากสารกึ่งตัวนำ เช่น ซิลิกอน และเจอร์เมเนียม ส่วนตัวนำไฟฟ้าที่ดี ความต่างศักย์ฮอลล์จะมีค่าน้อยกว่ามาก (เหตุผล พิจารณาได้จากสมการ (7) หรือสมการ (8) ในตอนท้าย)

จากสมการ (1) จะได้ว่า

รูป 2 การวัดความต่างศักย์ฮอลล์ V_H

เราสามารถวัด V_H โดยต่อ มิลลิโวลต์มิเตอร์เข้ากับจุด x และจุด y ดังรูป 2 ก

สภาพขั้วของ V_H ทราบได้จากเครื่องหมายที่อ่านได้จาก มิลลิโวลต์มิเตอร์

จากรูป 2 ก พาหะประจุคืออิเล็กตรอนจึงมีประจุลบ ถ้าพาหะประจุมีประจุบวก ทิศของ V_d และ E_H จะตรงข้ามกับในรูป 2 ก แต่ทิศของ F_B และ E_E ยังคงเดิม ดังแสดงในรูป 2 ข ทำให้ประจุบวกถูกผลักไปที่ขอบด้านขวา ส่วนประจุลบถูกผลักไปที่ขอบด้านซ้าย และสภาพขั้วของ V_H จะตรงข้ามกับกรณีที่พาหะประจุมีประจุลบ

จากรูป 1 ค ขณะที่แรงแม่เหล็กและแรงไฟฟ้ามีขนาดเท่ากัน เราจะได้

จากสมการ (2) จะได้

เนื่องจากอัตราเร็วลอยเลื่อน V_d มีค่า

เมื่อ n คือจำนวนพาหะประจุต่อลูกบาศก์เมตร (หรือความหนาแน่นของพาหะประจุ)

และ A คือพื้นที่หน้าตัดของแผ่นตัวนำบาง

แทนสมการ (5) ลงในสมการ (4) จะได้

เนื่องจาก คือความหนาของแผ่นตัวนำบาง ดังนั้น

สมการ (7) เขียนได้ใหม่เป็น

ปริมาณ V_HI และ t ในสมการ (8) หาได้จากการวัด ส่วนค่า n ขึ้นอยู่กับชนิดของวัสดุที่ใช้ทำหัววัด วัสดุที่เป็นสารกึ่งตัวนำจะมีจำนวนพาหะประจุน้อยกว่าตัวนำไฟฟ้าที่ดี แต่ก็ยังมีค่ามากพอที่จะทำให้เกิดกระแสไฟฟ้าที่สามารถวัดได้ ส่วนฉนวนมีจำนวนพาหะประจุน้อยมาก แต่ก็ยอมให้กระแสไฟฟ้าปริมาณเล็กน้อยผ่าน จากการศึกษาพบว่า สารกึ่งตัวนำที่เจือสิ่งเจือปนมีค่า n 10²²m^-3 และโลหะทั่วไปมีค่า n 10²⁸m^-3 ดังนั้น เราจึงสามารถหาความเข้มของสนามแม่เหล็กที่ไม่ทราบค่าจากสมการ (8) ได้

ความเข้มของสนามแม่เหล็กมีหน่วยในระบบเอสไอเป็นเทสลา (tesla) แทนด้วยสัญลักษณ์ T หน่วยเดิมของความเข้มของสนามแม่เหล็กคือ เกาส์ (gauss) แทนด้วยสัญลักษณ์ G โดยที่ 1T = 10⁴ G

---

ที่มา : รังสรรค์ ศรีสาคร สาขาวิชาฟิสิกส์ สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี